Kann ich L4/L5 überhaupt mit einem einzelnen vollständigen Hohmann Transfer erreichen?
Ich bin kein Spezialist in Orbitalmechanik, aber ich hatte im Kopf, dass der Hohmann Transfer zwischen zwei Planeten funktioniert. Also nur zwischen zwei Planeten, wenn diese auch zwei verschiedene Umlaufbahnen haben. Erde zu L4 sind jedoch keine zwei verschiedenen Umlaufbahnen. Sondern es ist die gleiche Umlaufbahn. Somit könnte ein (Anzahl = 1) Hohmann Transfer nicht möglich sein. (Vielleicht).
Idee zur Lösung:
- Man erstellt einen virtuellen Punkt L4V.
- Dieser L4V liegt auf einer Umlaufbahn 150% der Umlaufbahn der Erde.
- Man berechnet einen Hohmann Transfer von Erde zu L4V.
- Man fliegt zu L4V
- Man berechnet einen Hohmann Transfer von L4V zu L4.
- Man wartet auf L4V so lange, bis der Zeitpunkt optimal ist
- Man fliegt zu L4
So würde ich mir das vorstellen:
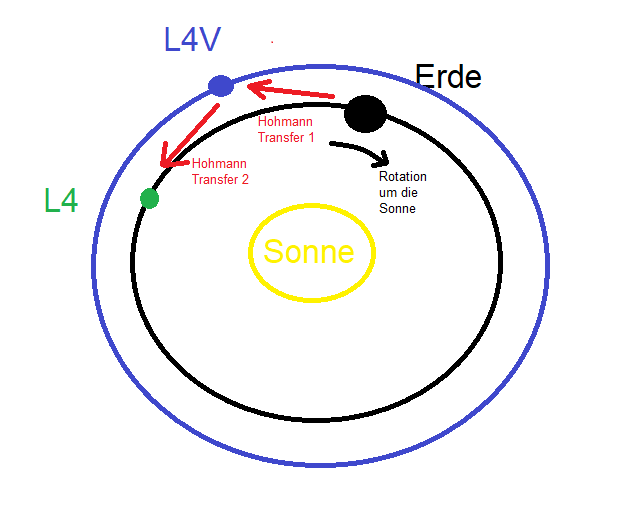
Das ganze kann man optimiere indem man es mit 130% und 150% und 170% ausprobiert. Verändern dürfte sich der Treibstoffbedarf und die Wartezeit auf L4V. Bei 130% ist auch die Frage, ob die Bahnverzerrung durch die hohe Gravitation der Erde nicht zu stärk stört. Aber vielleicht ist das auch erst bei 120% oder 110% der Fall.
Das ganze kann man noch weiter optimieren, indem man eine Transfer-Bahn beider Hohmann Transfers findet, welche beide vollständig gleich sind. Jetzt fliegt man zwei halbe Hohmann Transfers. Das könnte ein Zeit-Optimum sein.
So viel nur als Gedanken-Idee.