In dem Artikel wird die Anwendung von mehrfach reflektierten Lasern zwischen Quelle und Segel diskutiert. Grundannahme ist, dass ein Laser durch Beugung und Streuung nur eine bestimmte Wirkstrecke [TeX]L_{_{max}}[/TeX] hat, nach der er zu schwach und zu weit gestreut wurde. Durch mehrfache Reflexion wird diese verfügbare Strecke zwischen den Spiegeln schneller 'aufgebraucht', es wird aber auch eine höhere Beschleunigung erzielt, was den größeren Effekt erzielen soll.
Wurde da ein Fehler gemacht?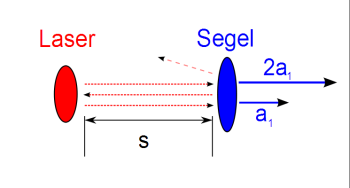
Meine Abbildung zeigt den Weg des Lichts bei dreifacher Reflexion.
Im einfachen Fall legt das Licht den Weg [TeX]l=s[/TeX] zurück und erzeugt bei einfachem Impulsaustausch die Beschleunigung [TeX]a=a_{_1}[/TeX].
Im Fall mit dreifacher Reflexion legt das Licht den dreifachen Weg [TeX]l=3s[/TeX] (hin-her-hin) zurück und hat zweimal eine Impulswechselwirkung am Segel [TeX]a_{_2}=2a_{_1}[/TeX]. Um die doppelte Beschleunigung zu erhalten, wir das Dreifache des wirksamen Lichtwegs 'verbraucht'.
In Formeln gilt bei konstanter Beschleunigung:
[TeX]v=at[/TeX]
[TeX]s=frac{1}{2}at^{^2}[/TeX]
Zusammen ergibt sich so die Abhängigkeit der Geschwindigkeit von Beschleunigung und Weg:
[TeX]v=sqrt{2as}[/TeX]
Wenn man die obigen Faktoren für die Beziehungen der Wege und Beschleunigungen zwischen beiden Fällen einsetzt, ergibt sich:
[TeX]v_{_2}=sqrt{frac{2}{3}}v_{_1}[/TeX]
Bzw. allgemein für n Reflexionen:
[TeX]v_{_n}=sqrt{frac{n-1}{n}}v_{_1}[/TeX],
so dass man im Grenzwert n-->inf wieder beim Ausgangsfall einer Reflexion landet ...
Und dabei ist noch kein Reflexionsgrad [TeX]mu<1[/TeX] eingeflossen ...
Damit gewinnt man durch mehrfache Reflexion (Multi-Bounce) nichts, man verliert sogar. Der wirksame Lichtweg wird "schneller aufgebraucht" als man zusätzliche Beschleunigung durch die Reflexionen erhält.
Habe ich einen Denkfehler?
