Ich habe mal ein wenig simuliert, um ein paar Flugbahnen zu zeigen, in unterschiedlichen Koordinatensystemen.
Annahmen:
- Start am Äquator
- Ziel ist ein polarer Orbit mit 90° Inklination im LEO
- die Rakete beschleunigt konstant mit 2g
- das Ganze wurde nur zweidimensional, kinematisch simuliert (also ohne Höhe, Erdkugel, Gravitation) ... es ist letztendlich der schrittweise Aufbau des Vektordiagramms ...
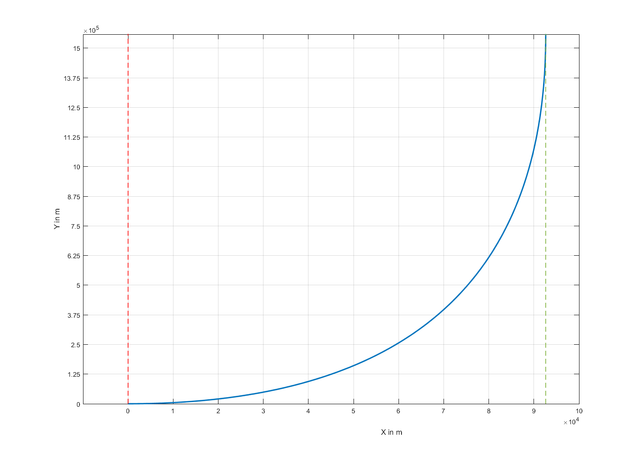
Der Graph zeigt die Bahn im intertialen Koordinatensystem, auf x- und y-Achse unterschiedlich skaliert. Ich bin praktisch ein im Raum ruhender Beobachter bei (0,0). Die rote Linie ist der 90°-Orbit über mir. Der Startort kommt mit ca. 465 m/s von links nach rechts unter mir durch und in dem Moment startet die Rakete. Sie steuert direkt und konstant den schrägen Kurs aus dem Vektordiagramm (hier 93,4°).
Die blaue Linie zeigt, was ich sehe. Die Rakete driftet weiter nach Osten, schwenkt (aus meiner Sicht) aber nach Norden. Sie erreicht 90° Flugrichtung am Ende des Graphen mit Orbitgeschwindigkeit, grüne Linie. Den 90°-polaren Orbit hat sie also "neben mit" erreicht, ca. 92km Versatz. Heißt: Um den roten Orbit über mir zu erreichen, muss sie ca. 199s früher starten, wenn der Zielorbit noch 92km im Osten liegt.
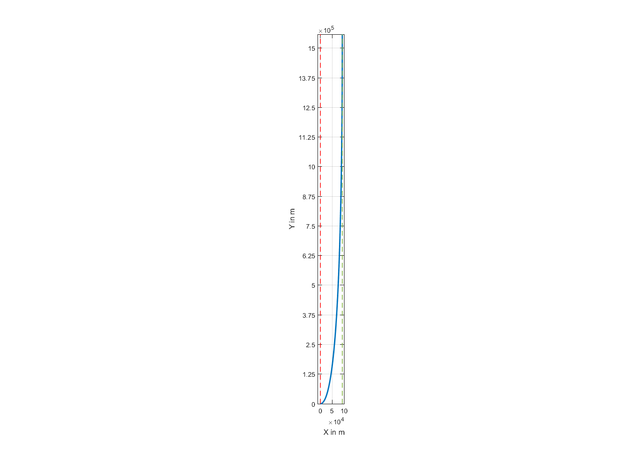
Hier noch das Bild mit "gleich skalierten Achsen", da sind die Größenordnungen zwischen der Ost- und Nordbewegung dann richtig/proportional.