Logarithmische Spiralen: Große / Kleine Wunder im UniversumSieht man auf den Taifun Rammasun (rechts im Bild) oder die 25 Millionen Lichtjahre entfernte Galaxie M101, so meint man, dass diese beiden Objekte nichts gemeinsam hätten.
Rammasun maß "nur" eintausend Kilometer im Durchmesser, während es die Galaxie M101 auf etwa 170.000 Lichtjahre bringt.
Echte Dimensionsunterschiede - ungeachtet der unterschiedlichen physikalischen Umgebung welche ihre Formgebung und Entwicklung beeinflußt.

Image Credit: M101 -
NASA,
ESA,
CFHT,
NOAO; Typhoon Rammasun -
MODIS,
NASA Ursprüngliche Idee des Vergleichs: Lawrence Anderson-Huang (
Ritter Astrophysical Obs., Univ. Toledo)
Irgendwie sehen sich beide Objekte sehr ähnlich und kommen einem irgendwie auch vertraut vor.
Beide mit Armen in Form einer schönen mathematischen Kurve, einer "Logarithmischen Spirale", bei denen also der Armabstand im entsprechenden geometrischen Verhältnis zum Abstand vom Zentrum wächst.
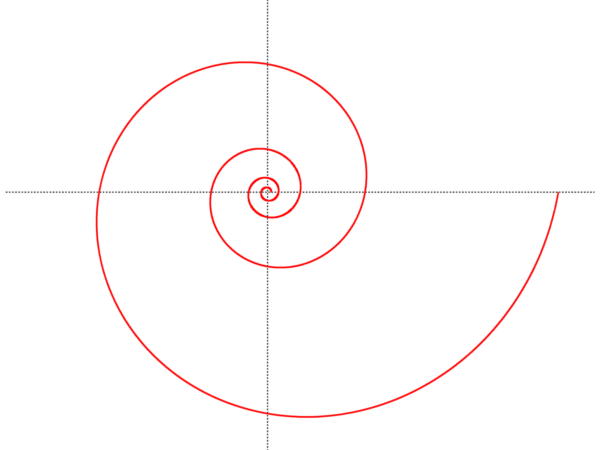
Bild-Quelle:
http://de.wikipedia.orgBei
Wikipedia findet man dazu: Eine logarithmische Spirale ist eine Spirale, die mit jeder Umdrehung den Abstand von ihrem Mittelpunkt, dem Pol, um den gleichen Faktor vergrößert. In umgekehrter Drehrichtung schlingt sich die Kurve mit abnehmendem Radius immer enger um den Pol. Jede Gerade durch den Pol schneidet die logarithmische Spirale stets unter dem gleichen Winkel.
Wegen dieser Eigenschaft spricht man auch von einer gleichwinkligen Spirale.
Diese "Gleichwinklige Spirale", im englischen auch als "growth spiral" bekannt, faszinierte Jakob Bernoulli so sehr, dass er sie "spira mirabilis" ("wundersame Spirale") nannte.
Die Bernoulli Spirale, wie sie auch genannt wird, fasziniert Mathematiker seit ihrer Entdeckung durch den Philosophen Descartes im 17. Jahrhundert.
Die logarithmische Spirale ist eine wunderbare Einrichtung in der Mathematik und zugleich auch in der Natur. Die logarithmische Spirale ist etwas Herrliches. Sie hat die Eigenschaft, dass sie aus einem exzentrisch gelegenen Mittelpunkt kommt und einen absoluten Mittelpunkt nicht erreichen kann.
Sie kreist ewig um eine Asymptote bzw. um eine Kegelschraubenbahn, die sie nicht in einem absoluten Zentrum erreichen kann. Das ist zunächst das wunderbare Kriterium dieser logarithmischen Spirale.
| Die Logarithmische Spirale in Polarkoordinaten dargestellt: | | Die Logarithmische Spirale in karthesischen (rechtwinkligen) Koordinatensystem: |
 | |  |
Kommt uns die Karthesische Darstellung bekannt vor?In der belebten Natur finden sich zahlreiche Beispiele logarithmischer Spiralen mit diversen Steigungen:
| Schneckenhäuser | |  |
| Ammoniten | |  |
| Samenanordnung der Sonnenblume (sogar in der Sonderform der Goldenen Spirale) | |  |
| der Fingerabdruck | |  |
| Balkenspiralgalaxie | |  |
Daneben finden sich annähernd logarithmisch spiralförmige Strukturen in allen dynamischen Mehrkörpersystemen
und fluiddynamischen Systemen (Wirbelbildung), sie beschreiben Wachstumsprozesse oder Spuren von subatomaren Partikeln in der Teilchenkammer.....
Beim weiteren Recherchieren zu diesem Thema bin ich auf
folgende Seite gestoßen, welche ein
Essay zur logarithmischen Spirale beinhaltet.
Es ist wirklich auffällig, dass im Lebensaufbau in allem die rechts- und linksdrehende logarithmische Spirale zu erkennen ist.
Also das Prinzip der Liebe, die Herzform. | Ein Herz aus Logarithmischen Spiralen | | Hier ein "Tränendes Herz" |
 | |  |
Abschließen möchte ich, tief im Eindruck des Erfahrenen und überwältigt von der Schönheit der Natur, ihren wundersamen Farben und Formen, mit Worten von Herrmann Hesse:
Wenn wir heute,
in einer Welt der Zwecke
und in einer Welt der Machbarkeiten,
nichts mehr hätten von der Phantasie,
von der Freude am Schönen,
von der Freiheit der Farben
und vom Schmücken der Räume,
dann wären wir mitten
in dem, was uns umgibt,
die ärmsten Menschen.
Hermann Hesse
-----------------------------------------------------------------
Quellen:
Mein Dank gilt insbesondere an
http://www.seniorenrunde-aktiv.de http://www.wikiweise.de/wiki/Logarithmische%20Spiralehttp://maven.smith.edu/%7Ephyllo/http://de.wikipedia.org/wiki/Logarithmische_Spirale